HARDY WEINBERG EQUILIBRIUM LAW
Introduction
The formula (p+q)2=p2+2pq+q2 is expressing the genotypic expectations of progeny in terms of gametic or allelic frequencies of the parental gene pool and is originally formulated by a British mathematician Hardy and a German physician Weinberg (1908) independently. Both forwarded the idea, called Hardy-Weinberg law equilibrium after their names, that both gene frequencies and genotype frequencies will remain constant from generation to generation in an infinitely large interbreeding population in which mating is at random and no selection, migration or mutation occur.
Should a population initially be in disequilibrium, one generation of random mating is sufficient to bring it into genetic equilibrium and thereafter the population will remain in equilibrium (unchanged in gametic and zygotic frequencies) as long as Hardy-Weinberg condition persists. Hardy-Weinberg law depends on the following kinds of genetic equilibriums for its full attainment :
- The population is infinitely large and mate at random.
- No selection is operative.
- The population is closed, i.e., no immigration or emigration occurs.
- No mutation is operative in alleles.
- Meiosis is normal so that chance is the only factor operative in gametogenesis
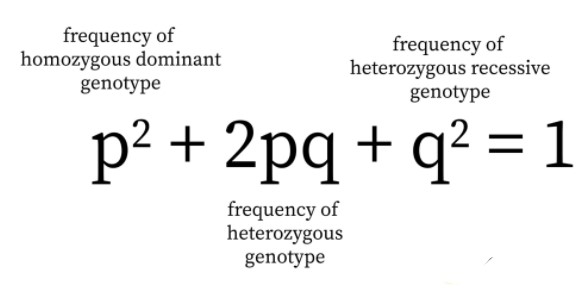
Genetic Equilibrium
As shown by Hardy and Weinberg, alleles segregating in a population tend to establish an equilibrium with reference to each other. Thus, if two alleles should occur in equal proportion in a large, isolated breeding population and neither had a selective or mutational advantage over the other, they would be expected to remain in equal proportion generation after generation. This would be a special case because alleles in natural populations seldom if ever occur in equal frequency.
They may, however, be expected to maintain their relative frequency, whatever it is, subject only to such factors as chance, natural selection, differential mutation rates or mutation pressure, meiotic drive and migration pressure, all of which alter the level of the allele frequencies. A genetic equilibrium is maintained through random mating.
Deviation From Hardy Wienberg Equilibrium
The Hardy-Weinberg explanation of equilibrium in the allele frequency pattern of a population required three assumptions–
- Individuals with each genotype must be as reproductively fit as those of any other genotype in the population.
- The population must consist of a large number of individuals.
- Random mating must occur throughout the population.
The Hardy-Weinberg theorem with its assumptions does not account for any change in allele frequency within populations. That is just what Hardy and Weinberg intended because their formula described the statics of a Mendelian population. Something more was required to formulate a mathematical explanation of change or dynamics in terms of allele frequencies. This need was filled by Fisher, Wright and J.B.S. Haldane, who provided additional theoretical models and superimposed the mechanisms for change in allele frequencies upon the Hardy-Weinberg equilibrium. Population statics was, thus, extended to become population dynamics.
The shifts or changes in gene frequencies can be produced by a reduction in population size, selection, mutation, chance (genetic drift), meiotic drive and migration.
Natural selection
Natural selection is generally believed to be the prominent agent for determining the relative frequency of alleles in a population. Natural selection differentiates between phenotypes in a population with respect to their ability to produce offspring. One phenotype may better survive endemic onslaughts of parasites or predators than another, one may penetrate new habitats more effectively than another; one may mate more efficiently than other; one may even prey on the other.
The important point is that some natural situation or environmental feature selectively allows one organism to develop and to propagate more efficiently, and one genotype is thereby afforded greater representation in the populations gene pool. If this selective process continues over many generations, allelic frequencies will change significantly and the potential will arise for evolutionary change.
Further, the natural selection process, while acting on the total phenotype, will, in fact, influence only the heritable portion of the phenotype. If a trait has a high heritability, selection can rapidly affect its frequency within a population, whereas selection will take a great deal longer to have any effect on a trait with a low heritability. Natural selection includes the following three parameters—survival rate, relative fitness and the selection coefficient.
To calculate values for these parameters and, thus, best understand their meaning, we can consider the data from a particular population. For simplicity we shall consider only a single gene locus in the population defined by the A and a alleles and we shall assume incomplete dominance, so that A/a heterozygote can be distinguished phenotypically from A/A, and a/a homozygotes. We then count the number of A/A, A/a, and a/a individuals in a given generation immediately before and immediately after some selective event—the introduction of a parasite, a change in temperature—has occurred
Mutation
Mutation is an evolutionary agent and mutability is a required property of the genetic material if evolution is to occur. One can visualize several ways that mutation might bring about evolutionary changes.
Mutation may be highly directed at a particular locus such that allele a1 is selectively driven to the a2 form. Alternatively, the mutation process might be random but with time the a2 form would come to predominate over a1. Finally, mutation might simply provide a population with new alleles (new mutational “currency”) on which any and all evolutionary agents (natural selection, for example) can act.
Meiotic Drive and Migration Pressure
Besides directional selection (natural and artificial) and mutation pressure, meiotic drive and migration pressure are two agents that can shift gene frequencies in a population out of a Hardy Weinberg equilibrium.
1. Meiotic drive :- The Hardy-Weinberg concept of an equilibrium population assumes that alleles will segregate in a 1 : 1 fashion at meiosis and that all gametes in the pool have an equal probability of fertilizing one another. Clearly, if gametes of genotype a1 have greater success in fertilization than gametes of genotype a2 the frequency of a1 in the population should increase as a2 decreases. Such a mode of bringing about potential evolutionary change is in many respects a form of natural selection but it has earned the specific designation of meiotic drive.
Normal segregation ratios can be biased by a number of factors. The most extensively studied example is the segregation distorter (SD) locus in D. melanogaster : a +/SD heterozygous male transmits to his offspring many SD alleles than + alleles.
A high prevalence of SD might, therefore, be expected in natural populations, but the allele is, in fact, uncommon, its frequency being less than 0.1. Some additional selective pressures, thus, appear to counteract meiotic drive at this particular locus presumably by agents that act against SD-carrying flies. The existence of meiotic drive is not easy to demonstrate experimentally. However, its specific role in evolution is still unassessed.
2. Migration pressure :- Perhaps the most obvious way that gene frequencies in a population can be changed is the introduction of new individuals with new genotypes, a process known as migration pressure. The effect of migration pressure can be expressed mathematically as follows.
In a population we can call X a particular gene is present with a frequency qx. A certain number of individuals from this population now migrate and join population Y in which the gene in question is present at frequency qY.
The immigrant, thus, comes to represent some fraction m of the total number of individuals present in the expanded version of population Y and a new gene frequency, q´Y, becomes established. The value of q´Y, will be equal to the contribution made by the immigrants (qxm) plus the contribution made by the original population [qY (1–m)], where 1–m represents the proportion of non-migrants.
Therefore, q´Y = qX m+qY (1-m) and the change in q after one generation in such a population becomes ∆q = q´Y –qY = qY –mqY +mqX –qY = – m (qY –qX ) when numerical values are substituted into this equation, it becomes clear that significant changes in the value of q can result if these two populations differ only slightly in the frequency of a given gene and if only a moderate degree of migration occurs between them.
Random Genetic Drift
Random fluctuation in allele frequencies, called genetic drift, also occurs in breeding populations. The effect of genetic drift is negligible in large populations but in small breeding populations all the limited number of progeny might be of the same type with respect to certain gene pairs because of chance alone. Should this happen, fixation or homozygosity will have occurred at the locus concerned. Fixation is defined as gene frequency reaching p = 1.00 or q = 1.00. Chance fluctuations may or may not lead to fixation
Conclusion
The modifications in the frequency of alleles in a given population over generations are termed evolution. In contrast, the population in Hardy Weinberg is defined as not evolving. The equation derived based on the Hardy Weinberg equilibrium concept is called the Hardy Weinberg equation. In this particular equation, p is represented as the dominant allele’s frequency and q is the representation of the recessive allele’s frequency.
This is explained with an example to conclude a Hardy Weinberg equation. Consider a single locus with the presence of only two alleles namely A and a. The A’s frequency is represented as ‘p’ and the a’s frequency is represented as ‘q’. Thus, the expected frequency of genotype in random mating under limited conditions are:
f(aa) = aa homozygotes are q2
f(AA)= AA homozygotes are p2
f(Aa) = heterozygotes are 2pq
From the above, the Hardy Weinberg equation is represented as p2 + q2 + 2pq = 1. The frequencies of alleles p and q remain constant without any influence such as migration, genetic drift, mutation, natural selection. These steady conditions help in attaining the equilibrium state.
Discover more from ZOOLOGYTALKS
Subscribe to get the latest posts sent to your email.

