Mean, median and mode all three are Central Tendency or Averages. The Arithmetic mean lies under Mathematical Average and the other two Median and Mode are types of Positional Averages.
“A measure of central tendency is a typical value around which the figures congregate”. The value of central tendency or average always lies between the minimum and maximum values.
MODE
Mode is the value of the variable which occurs most frequently in a distribution. Mode is also positional average which can be located by inspection.
- Unimodal- When distribution has one concentration of frequency.
- Bimodal- when it has two concentrations.
- Trimodal- when it has three concentrations.
CALCULATION
FOR INDIVIDUAL OBSERVATIONS
Step – The data is arranged into a discrete series. So, that the value which has the highest frequency can be known.
For example:

In this data 60 is repeated 5 times. So, mode is 60.
DISCRETE SERIES :
Step : Which variable (x) has the highest frequency (f) is the Mode.

Solution :
Here, the value 45 is repeated 5 times.
So, mode is 45.
Sometimes we cannot depend on this method of inspection to find out mode. In such conditions , prepare grouping and analysis table to found out mode.
CONTINUOUS SERIES
Step 1: In this case of bimodal series or trimodal series we prepare.
Form grouping and analysis table and then find out highest frequency.
Step 2: Apply the formula
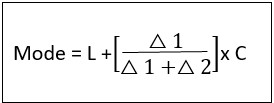
Where,
L = lower limit of the modal class
△1= the difference between the frequency of the modal class and the preceding modal class (f1 – f0)
△2= the difference between the frequency of the modal class and the succeeding modal class ( f1 – f2)
c = class interval of modal class.
f1 = frequency of the modal class.
f0 = frequency of preceding modal class.
f2 = frequency of the succeeding modal class
OTHER FORMULAE FOR MODE :
Mode = 3 Median – 2 Mean
Mode = Mean – 3 (Mean -Mode)
Mean – Mode = 3( Mean- Median)
MERITS OF MODE
- Very easy to understand.
- Calculation is simple.
- It remains unaffected by extreme values.
- It is a positional average like median, and can be located easily by inspection.
- Graphic method is also used to determine Mode.
DEMERITS OF MODE
- It is ill-defined and indeterminate.
- It cannot be used in algebraic calculations.
- In bimodal class, the calculation is difficult.
- It is not based on all observations.
Related
Discover more from ZOOLOGYTALKS
Subscribe to get the latest posts sent to your email.

